Сумма ряда обратных квадратов (Basel problem)
 В истории математики имеется много случаев, когда кто-либо ставил задачу перед математическим миром в целом, и эта задача оставалась нерешенной в течение десятилетий или даже веков. Часто в процессе решения такой задачи появлялись новые области математики.
В истории математики имеется много случаев, когда кто-либо ставил задачу перед математическим миром в целом, и эта задача оставалась нерешенной в течение десятилетий или даже веков. Часто в процессе решения такой задачи появлялись новые области математики.
Этот пост – рассказ об одном из таких случаев, так называемой Basel problem (задаче о сумме ряда обратных квадратов, Базель – город в Швейцарии), впервые поставленной в качестве вызова европейским математикам в 1644 году. Она сопротивлялась всем попыткам ее решить до тех пор, пока молодой Леонард Эйлер в 1734 году не нашел ответ. Как увидит читатель, решение Эйлера – работа удивительной изобретательности, хотя уровень математики не превосходит в ней начального курса алгебры.
Задача
Basel problem формулируется просто: требуется найти точное значение следующей бесконечной суммы:
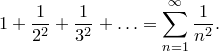
Как и для всех остальных бесконечных рядов, для этого ряда возникает вопрос, сходится ли он к конечному значению. Тот факт, что его члены становятся бесконечно малыми, не является достаточным для обеспечения сходимости. Например, следующий ряд
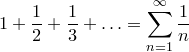
имеет бесконечную сумму, т.е. расходится, несмотря на то, что его члены становятся сколь угодно малыми (этот ряд называется гармоническим, и доказательство его расходимости приведено ниже).
Тем не менее, для ряда обратных квадратов ранее было показано, что он сходится к числу, меньшему 2, только не было известно точное значение, к которому он сходится.
Два соперника и их учитель делают безуспешную попытку
Первыми математиками мирового уровня, пытавшимися решить Basel problem, были швейцарцы, братья Якоб Бернулли (1654-1705) и Иоганн Бернулли (1667-1748). Задача названа так, потому что Базель – их родной город. Бернулли были среди первых, кто понял и начал применять новое исчисление, о котором они узнали от Готфрида Лейбница (1646-1716), – одного из его авторов. К 1690 году они считались ведущими европейскими математиками. К сожалению, к этому времени они стали ожесточенными, непримиримыми соперниками, и казалось, испытывали практически убийственную ненависть друг к другу. Каждый из них мог бы лгать, воровать, пошел бы на плагиат, если бы это помогло ему казаться лучше другого. Соперничество не прекратилось даже со смертью Якоба – Иоганн пытался выдать некоторые неопубликованные работы своего покойного брата за свои собственные, и он также отказался помочь опубликовать трактат Якоба по теории вероятности, опасаясь, что это поднимет репутацию брата. По крайней мере, Иоганн, вполне возможно, был просто… нехорошим человеком – когда его собственный сын Даниил позже выиграл математический приз, за который Иоганн также боролся, он выгнал Даниила из дома и лишил его наследства.
В течение многих лет братья Бернулли пытались решить задачу о сумме ряда обратных квадратов, что, вероятно, частично было обусловлено желанием победить соперника, но они не добились успеха. Лейбниц также работал над проблемой в течение многих лет и не получил никакого результата.
Вступление Эйлера
Леонард Эйлер (1707-1786) родился в Базеле, и так случилось, что его отец знал Иоганна Бернулли. Когда Леонарду было 14 лет, его отец попросил Иоганна, чтобы тот учил юношу математике. Иоганн нехотя согласился, но затем быстро обнаружил, что его новый ученик имеет способности, превосходящие все те, какие он когда-либо видел. Вскоре роли поменялись, и Иоганн учился у Эйлера. Иоганн посоветовал отцу Леонарда отказаться от идеи сделать Леонарда министром, предложив ему стать математиком. К чести его, отец согласился.
Через несколько лет Эйлер занял пост в Академии в Санкт-Петербурге, в России. Именно там, в 1734 году, Эйлер нашел решение Basel problem. В результате его сразу же стали считаеть ведущим математиком Европы.
Решение
Для начала рассмотрим алгебраическое уравнение, степень которого я произвольно полагаю равной четырем:
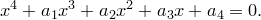
Предположим, что его корни 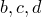 и
и  . Тогда мы можем разложить полином на линейные множители следующим образом:
. Тогда мы можем разложить полином на линейные множители следующим образом:
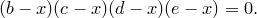
Если ни один из этих корней не равен нулю, мы можем записать также
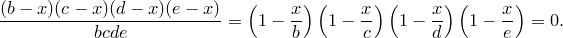
Далее, имеются некоторые полиномы бесконечной степени, например,
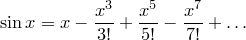
Эти особые бесконечные ряды были открыты Ньютоном, и довольно легко вывести такие разложения с помощью математического анализа. Здесь я буду считать его известным. Мы знаем нули синуса, это 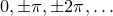 Первой идеей Эйлера было предположение, что теорема о разложении на множители верна для бесконечных полиномов, т.е.
Первой идеей Эйлера было предположение, что теорема о разложении на множители верна для бесконечных полиномов, т.е.
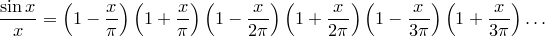
Заметим, что каждая пара множителей 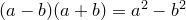 и перепишем равенство
и перепишем равенство
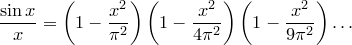
Теперь Эйлер получил, что бесконечная сумма равна бесконечному произведению!? (также обратите внимание на знаменатели в этом произведении – в них имеются квадраты натуральных чисел, что намекает о присутствии где-то здесь ряда обратных квадратов).
Хотя произведение состоит из бесконечного числа множителей, мы можем выяснить, какой коэффициент будет при каждой степени 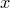 . Рискуя обидеть читателя, я все же объясню: рассмотрим конечное произведение
. Рискуя обидеть читателя, я все же объясню: рассмотрим конечное произведение
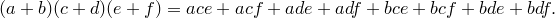
Каждый элемент при раскрытии скобок в произведении, скажем 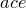 , равен произведению слагаемых, взятых из каждой скобки слева по одному. Так, Эйлер увидел, что в нашем бесконечном произведении член, содержащий
, равен произведению слагаемых, взятых из каждой скобки слева по одному. Так, Эйлер увидел, что в нашем бесконечном произведении член, содержащий 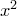 , будет равен
, будет равен
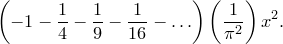
Однако, поскольку бесконечное произведение равно бесконечному ряду для 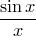 , коэффициент при
, коэффициент при 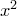 должен быть равен
должен быть равен 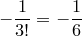 . Приравняем коэффициенты и умножим полученное равенство на
. Приравняем коэффициенты и умножим полученное равенство на 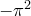 , получим
, получим
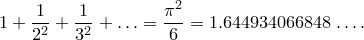
Итак, через 90 лет был найден ответ. Он остается одним из самых странных, самых удивительных результатов в математике. Мы связываем постоянную 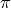 с кругами, а Basel problem содержит обратные квадраты. И что здесь вдобавок делает синус из тригонометрии? Когда Иоганн Бернулли увидел решение Эйлера, он должен был сказать: “Был бы только мой брат жив, чтобы увидеть это’’. Возможно, Иоганн смягчился с годами.
с кругами, а Basel problem содержит обратные квадраты. И что здесь вдобавок делает синус из тригонометрии? Когда Иоганн Бернулли увидел решение Эйлера, он должен был сказать: “Был бы только мой брат жив, чтобы увидеть это’’. Возможно, Иоганн смягчился с годами.
Это не все, что установил Эйлер в своей исторической работе. Используя подобные методы, он показал, что
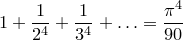
и
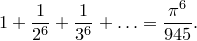
Оставался очевидный вопрос: а что с нечетными степенями натуральных чисел? Оказывается, что подобные методы не работают для нечетных степеней. В течение всей своей жизни Эйлер много раз пытался найти эти суммы, но ему этого сделать не удалось. В конце концов он просто сказал: “Задача представляется сложной’’. Когда Эйлер сказал о математической задаче, что она сложная, обычным математикам, вероятно, не стоит заботиться о ее решении. И конечно же, сегодня, спустя 200 с лишним лет, эти суммы не найдены.
Следствия
Практики могут задать вопрос, оправданы ли все эти усилия, принесшие результат, не имеющий никакой очевидной пользы. Простой ответ состоит в том, что эта задача из теории чисел, а в теории чисел подобные вопросы просто не возникают. Менее циничным ответом будет тот, что теория чисел иногда находит свой путь в реальный мир. Хорошим примером тому является теорема Ферма, открытая им в 1640 году, так называемая малая теорема Ферма. На этом абстрактном результате основан алгоритм криптографии, который применяется в Интернете для передачи секретной информации, такой как номера кредитных карт. Без него электронная коммерция была бы невозможна.
Что касается задачи о сумме ряда обратных квадратов, то позже оказалось, что она тесно связана с гипотезой Римана, которая сегодня считается одной из самых важных нерешенных проблем в математике. Эта гипотеза была предложена в 1859 году. Она считается верной, но до сих пор ее еще никто не доказал. Нам нужен новый Леонард Эйлер.
Приложение. Расходимость гармонического ряда
Как было написано выше, это ряд:
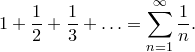
Якоб Бернулли доказал, что эта сумма бесконечна. Якоб заметил, что ряд может быть разделен на группы слагаемых:
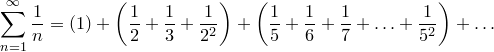
Он предположил, что сумма слагаемых в каждой группе единица или больше. Если так, то сумма гармонического ряда бесконечна, поскольку она равна сумме бесконечного числа слагаемых, каждое из которых единица или больше (групп бесконечно много). Чтобы доказать предположение, рассмотрим одну группу без первого слагамого:
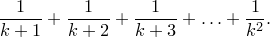
Число слагаемых в этой группе равно 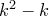 . Наименьшее слагаемое – последнее, так что
. Наименьшее слагаемое – последнее, так что
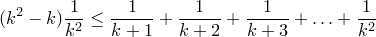
или
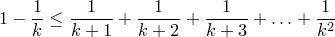
Добавляя 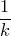 к обеим частям равенства, получаем требуемый результат.
к обеим частям равенства, получаем требуемый результат.